#wannabeeeeeee the best DataScientist
2장. 기계 학습 본문
728x90
📊 기계학습에서 수학이 하는 일
기계학습(Machine Learning)은 단순히 데이터를 처리하는 기술이 아니라, 수학을 기반으로 문제를 정의하고 해결하는 과정입니다. 특히 목적함수를 설정하고, 최적의 해를 찾아가는 최적화 과정에서 수학은 핵심적인 역할을 합니다.
수학이 기계학습에서 중요한 이유
- 모델의 목적함수 정의
예: 평균제곱오차(MSE), 교차엔트로피(Cross-Entropy)
→ 모델이 잘 작동하도록 평가하는 기준 - 최적화 이론 제공
→ 미분, 편미분, 선형대수, 확률론 등의 수학적 도구를 사용하여
모델이 목표값을 최대한 정확히 예측하도록 학습함
정보 이론 (Information Theory)
▶ 핵심 개념: "확률이 작을수록 더 많은 정보를 가진다"
즉, 예측하기 어려운 사건일수록 정보량이 크다는 의미입니다.
🔹 엔트로피(Entropy)
- 확률변수의 불확실성이나 무질서 정도를 수치화
- 예시:
- 윷놀이는 '모', '윷' 등 확률이 다름
- 주사위는 1~6이 동일 확률 → 더 예측하기 어려움 → 엔트로피 ↑
🔹 교차 엔트로피 (Cross-Entropy)
- 모델이 예측한 분포와 실제 정답 분포의 차이를 측정
- 딥러닝에서 MSE보다 더 자주 사용됨 (특히 분류 문제에서)
🔹 KL 다이버전스 (Kullback–Leibler Divergence)
- 두 확률 분포 간의 차이(비대칭적 거리)를 계산
- 실제 분포(P)와 모델 예측(Q) 간의 차이
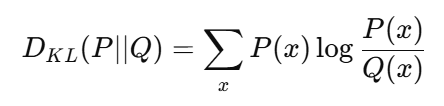
💡 Cross-Entropy와 KL Divergence는 함께 사용됨
Cross-Entropy = 실제 분포의 엔트로피 + KL Divergence
최적화 (Optimization)
▶ 수학적 최적화 vs 기계학습 최적화
구분수학적 최적화기계학습 최적화
| 대상 함수 | 일반 함수 (보통 수식으로 주어짐) | 훈련 데이터 기반으로 구성된 목적함수 |
| 방법 | 미분, 라그랑주 승수 등 | 경사 하강법(Gradient Descent), Adam 등 |
| 목적 | 수학적으로 최소/최대값 찾기 | 예측 정확도가 높은 파라미터 찾기 |
미분과 경사 하강법
🔹 편미분과 그레이디언트(Gradient)
- 여러 변수 함수에서 특정 변수만 미분 → 편미분
- 이들을 벡터로 모은 것이 그레이디언트
→ 함수가 가장 빨리 증가하는 방향을 알려줌
🔹 경사 하강법 (Gradient Descent Algorithm)
"언덕을 내려가는 방식으로 목적함수를 최소화"
- 초기 파라미터 설정
- 그레이디언트 계산
- 음의 방향으로 이동
- 이 과정을 반복 → θ:=θ−η⋅∇J(θ)
- θ : 파라미터
- η : 학습률(learning rate)
- ∇J(θ) : 목적함수의 그래디언트
💡 학습률이 너무 크면 발산하고, 너무 작으면 느리게 수렴
회귀분석 (Regression Analysis)
🔹 회귀 모형의 종류
모형설명
| 단순 선형 회귀 | 독립변수 X 하나, 종속변수 Y 하나 |
| 다중 선형 회귀 | 여러 개의 X → Y 하나 |
| 다변량 회귀 | 여러 개의 X → 여러 개의 Y |
🔹 최소제곱법 (Least Squares Method)
- 잔차(예측값 - 실제값)의 제곱합을 최소화
- 선형회귀에서 사용되는 기본적인 방법

- 이 식이 바로 평균제곱오차(MSE) 목적함수입니다.
🔹 MSE vs Cross-Entropy
목적함수사용 분야특징
| MSE | 회귀 문제 | 연속형 값 예측, 간단하지만 분류에 부적합 |
| Cross-Entropy | 분류 문제 | 확률 분포 예측 정확도 평가에 우수 |
✅ 마무리 요약
- 기계학습은 수학 없이는 성립할 수 없습니다.
- 수학은 모델의 구조를 세우고, 데이터를 통해 배울 수 있는 기반을 제공합니다.
- 정보이론은 모델이 얼마나 잘 예측하는지 정의하고,
최적화 이론은 그 목표에 얼마나 빨리 도달할지를 결정합니다.
728x90
'Master's degree > 머신러닝Ⅰ' 카테고리의 다른 글
| 4장. 딥러닝 기초 (0) | 2025.05.23 |
|---|---|
| 3장. 다층 퍼셉트론 (0) | 2025.05.09 |
| 1장. 소개 (0) | 2025.04.04 |
| 기계학습에 필요한 선형 대수 (0) | 2025.03.09 |




