#wannabeeeeeee the best DataScientist
회귀분석(1) 본문
◎ 회귀분석
ㅡ 회귀분석이란 : 입력 변수인 X의 정보를 활용하여 출력 변수인 Y를 예측하는 방법
ㅡ 단순 선형 회귀분석

- B0는 절편, B1은 기울기이며 합쳐서 회귀계수(coefficients)로도 부른다.
◎ 회귀계수 추정
ㅡ 실제 값과 우리가 추정한 값의 차이가 적으면 적을수록 좋을 것
ㅡ 실제 값과 우리가 추정한 값의 차이를 잔차(residual)라고 하며 이를 최소화하는 방향으로 추정

ㅡ SSE B0과 B1로 편미분 하여 연립방정식을 푸는 방법(Least Square Method)

◎ 회귀계수의 의미

# 위의 식에서 B1의 해석 : X가 1 단위 증가할 때마다 y가 B1만큼 증가한다.
○ 선형 회귀의 정확도 평가
- 잔차의 제곱합(SSE)을 최소화하는 방법으로 회귀 계수를 추정
- SSE가 작으면 작을수록 좋은 모델이라 볼 수 있다
- MSE(Mean Squared Error)는 SSE를 표준화한 개념


※ Y의 총 변동(SST)은 회귀 직선으로 설명 불가능 한 변동(SSE)과 회귀 직선으로 설명 가능한 변동(SSR)으로 이루어짐

※ R²은 설명력으로 입력 변수인 X로 설명할 수 있는 Y의 변동을 의미 (0 <= R² <= 1)
+ R² 이 1에 가까울수록 선형 회귀 모형의 설명력이 높다는 것을 뜻한다.
※ 변수가 여러 개일 때 각각 Y를 설명하는 변동성이 크면 좋은 변수 -> p-value는 자연스레 낮아진다.
○ 단순 선형 회귀분석의 검정


◎ 다중 선형 회귀분석
- 단순 선형 회귀분석 : 변수가 1개인 경우
- 다중 선형 회귀분석 : 변수가 여러 개인 경우

○ 다중 선형 회귀분석의 검정 : 단순 선형 회귀분석과 동일하다.
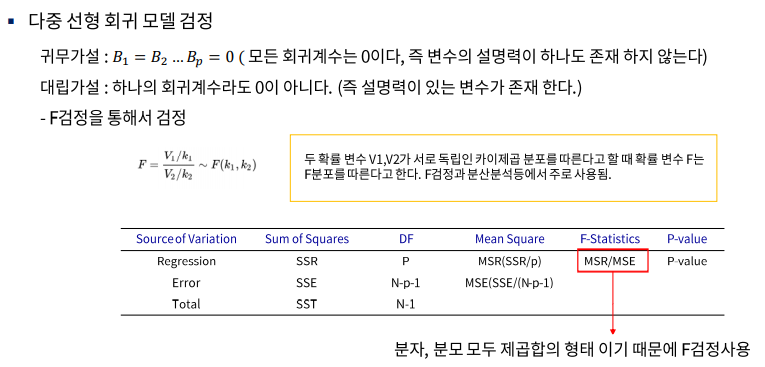
○ 다중 선형 회귀 모델 검정
○ 다중공선성(Multicollinearity) : 독립변수들이 강한 선형 관계에 있을 때 다중공선성이 있다고 한다.


○ 다중공선성 진단 방법
ⓐ VIF가 10 이상인 경우 다중공선성이 있는 변수라고 판단!!

ⓑ 상관 행렬 및 산점도를 보고 판단
# 다중공선성을 근본적으로 해결하는 방법은 아직 없다..
◎ 회귀모델의 성능지표
※ R²은 변수가 증가하면 증가할수록 R² 는 자연스레 증가한다.
● Adjusted R²
- 변수 수가 증가하는 만큼 penalty를 주는 지표가 Adjusted R²

● AIC (Akaike information criterion)
- 모델의 성능지표로서 MSE에 변수 수만큼 penalty를 주는 지표

● BIC (Bayes information criteria)
- AIC의 단점은 표본 n이 커질 때 부 정확해지므로 이를 보완한 지표가 BIC

◎ 모형의 성능지표
● MSE (Mean Squared Error)
-예측한 값이 실제 값과 유사한지 평가하는 척도가 필요
- MSE는 실제 종속 변수와 예측한 종속 변수 간의 차이
- MSE는 작을수록 좋지만, 과도하게 줄이면 과적합의 오류를 범할 가능성이 높아진다.

● MAPE (Mean absolute percentage error)
- MAPE는 퍼센트 값을 가지며 0에 가까울수록 회귀 모형의 성능이 좋다고 해석할 수 있다.- 0% ~ 100% 사이의 값을 가져 이해하기 쉬우므로 성능 비교 해석이 가능

○ 이산형 확률변수 일 때
● 정확도 (Accuracy) : 전체 데이터 중에서 모형으로 판단한 값이 실제 값과 부합하는 비율
● 정밀도 (Precision) : 분류 모형이 불량을 진단하기 위해 얼마나 잘 작동했는 지표
● 재현율 (Recall) : 불량 데이터중 실제로 불량이라고 진단한 제품의 비율
● 특이도 (Specificity) : 분류 모형이 정상을 진단하기 위해 잘 작동하는지를 보여주는 지표


◎ 변수 선택법
- 변수가 여러 개일 때 최적의 변수 조합을 찾아내는 기법
⑴ Feedforward Selection 방법 : 변수를 추가해가며 성능지표를 비교해가는 방법

⑵ Backward Elimination 방법 : 변수를 제거해가며 성능지표를 비교해가는 방법

⑶ Stepwise 방법 : 가장 유의한 변수를 추가하거나 유의하지 않는 변수를 제거해나가는 방법

◎ 교호작용
- 변수 간의 시너지 효과
◆ 명목형 변수(Dummy variable) : 성별, 대학, 지역 등 명목형 변수의 경우 전처리가 필요함.

◎ 회귀분석의 진단
- 과연 이 회귀모델이 잘 만들어진 모델인 것인가에 대한 진단이 필요
- 회귀분석에서는 아래 잔차에 대한 세 가지 가정이 존재 : 정규성, 독립성, 등분산성


◎ 다항회귀분석
- 독립변수와 종속 변수 간의 비선형 관계를 가질 경우 다항회귀분석 사용
- Residual Plot을 통해 다중 회귀의 가정이 위배된 경우 다항회귀분석 사용

'Data scientist > Machine Learning' 카테고리의 다른 글
| 회귀분석(3)_변수선택법 Code (0) | 2021.08.21 |
|---|---|
| 회귀분석(2)_Code (0) | 2021.08.19 |
| 수학적 개념 이해(2) (0) | 2021.08.19 |
| 수학적 개념 이해(1) (0) | 2021.08.19 |
| Machine Learning_basic(2) (0) | 2021.08.18 |




