◎ 인공 지능 : 기계가 사람의 행동을 모방하게 하는 기술
◎ 기계 학습 : 데이터로부터 학습하여 실행할 수 있도록 하는 알고리즘을 개발하는 연구 분야
◎ 딥러닝 : 기계 학습의 한 분야인 인공 신경망에 기반하여, 많은 양의 데이터를 학습해 뛰어난 성능을 이끌어내는 연구 분야



◎ 퍼셉트론 : 신경 세포를 이진 출력의 단순 논리 게이트로 해석하여 고안한 퍼셉트론 (Perceptron)

◎ 활성 함수 : 퍼셉트론의 출력에 의미를 부여해 주며, 일반적으로 비선형(Non-linear) 함수이다.




※ Sigmoid는 하나의 입력을 0으로 강제한 2-Class Softmax 함수와 동일하다.

◎ 손실 함수 : 지도 학습 알고리즘에 반드시 정의되어야 한다.
+ 딥러닝 알고리즘 학습의 길잡이로서 손실 함수가 필요하다.

● 평균 제곱 오차 함수(MSE) : 가장 기본적인 손실 함수. 오차가 커질수록 손실 함수가 빠르게 증가하는 특징

● 평균 절대 오차(MAE) : 오차가 커져도 손실 함수가 일정하게 증가하는 특징이 있다. Outlier에 강건한 특징이 있다. 통계적으로 중간 값(Median)과 연관이 있다.

● 교차 엔트로피 오차(CEE) : 원-핫 인코딩으로 인해, 정답인 클래스에 대해서만 오차를 계산, 정확히 맞추면 오차가 0, 틀릴수록 오차가 무한히 증가하는 특징이 있다.

◎ 신경망 구조 : 신경망은 뉴런을 기본 단위로 하며, 이를 조합하여 복잡한 구조를 이룬다.
● Fully-Connected Layer(전결합 계층) : 두 계층 간의 모든 뉴런이 연결되어 있는 계층을 뜻한다.
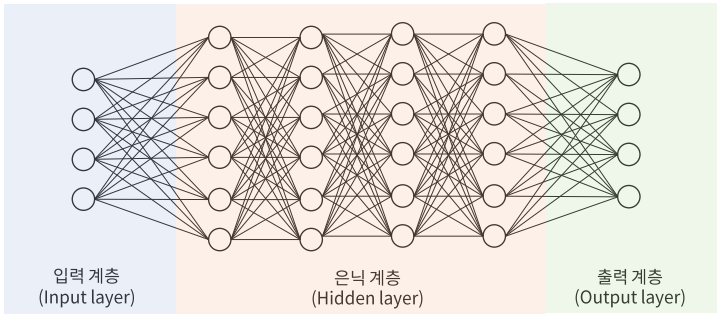
● 얕은 신경망(Shallow Neural Network) : 입력 계층, 은닉 계층, 출력 계층으로 이루어진 신경망, 심층 신경망의 등장 이후 기존의 신경망을 '얕은' 신경망으로 부름, 각 계층은 Fully-connected layer로 이루어져 있음

● 심층 신경망(Deep Neural Network; DNN) : 얕은 신경망보다 은닉 계층이 많은 신경망을 DNN이라고 부른다. 보통 5개 이상의 계층이 있는 경우 '깊다'라고 표현
◎ 최적화 이론

● 분석적 방법(Analytical method) : 함수의 모든 구간을 수식으로 알 때 사용하는 수식적인 해석 방법
● 수치적 방법(Numerical method) : 함수의 형태와 수식을 알지 못할 때 사용하는 계산적인 해석 방법

※ 딥러닝 네트워크의 학습은 손실 함수가 최소가 되게 하는 파라미터를 구하는 최적화 문제로 볼 수 있다.
◎ Gradient Descent(경사 하강법)
● 무차별 대입법 (Brute-force) : 가능한 모든 수를 대입해 보는 방법, 가장 단순한 방법
+ x(최적값)이 존재하는 범위를 알아야 함, x를 정확히 찾기 위해 무한히 촘촘하게 조사해야 함
● 경사 하강법 : f(x)의 값이 변하지 않을 때 까지 스텝을 반복한다.
+ 기울기(Gradient)는 스칼라를 벡터로 미분한 것이며, 벡터의 각 요소로 미분하면 된다.

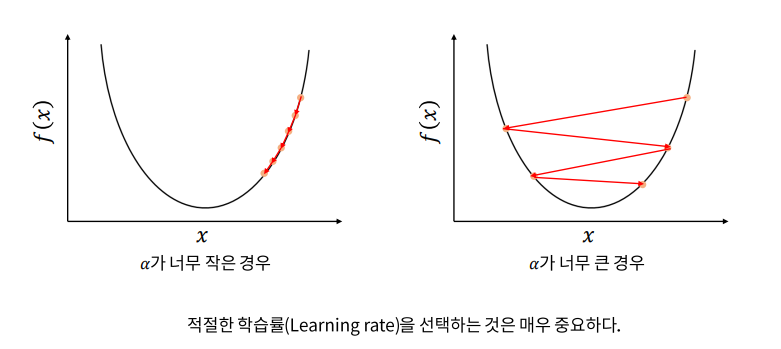
※ 볼록 함수는 어디서 시작하더라도 경사 하강법으로 최적 값에 도달할 수 있다.
※ 비볼록 함수는 시작 위치에 따라 다른 최적 값을 찾는다. 즉, Local minimum에 빠질 위험이 있다.

● Momentum : 돌이 굴러 떨어지듯, 이동 벡터를 이용해 이전 기울기에 영향을 받는 알고리즘
+ 관성(Momentum)을 이용하면 Local minimum과 잡음에 대처할 수 있다. 이동 벡터(vt)를 사용하므로, 경사 하강법 대비 2개의 메모리 사용

● AdaGrad : 적응적 기울기는 변수별로 학습율이 달라지게 조절하는 알고리즘
+ 기울기가 커서 학습이 많이 된 변수는 학습율을 감소시켜, 다른 변수들이 잘 학습되도록 한다. gt가 계속해서 커져서 학습이 오래 진행되면 더이상 학습이 이루어지지 않는 단점이 있다.

● RMSProp : AdaGrad의 문제점을 개선한 방법으로, 합 대신 지수평균을 사용
+ 변수 간의 상대적인 학습율 차이는 유지하면서 gt가 무한정 커지지 않아 학습을 오래 할 수 있다.

● Adam : RMSProp과 Momentum의 장점을 결합한 알고리즘
+ 가장 최신의 기술이며, 딥러닝에서 가장 많이 사용된다.

'Data scientist > Deep Learning' 카테고리의 다른 글
| Deep Learning_3 (0) | 2021.09.21 |
|---|---|
| Deep Learning_2 (0) | 2021.09.16 |