◎ 역전파 알고리즘


※ 심층 신경망의 각 Layer를 하나의 함수로 본다면, 신경망을 합성 함수로 표현할 수 있다.

※ 미분의 연쇄 법칙과 각 함수의 수식적 미분을 이용하면, 단 한 번의 손실 함수 평가로 미분을 구할 수 있다.
※ 역전파 알고리즘의 문제점 :
1. 기울기 소실 문제 : 역전파 계층이 많아질 수록 학습이 잘 되지 않는다.




◎ 뉴럴 네트워크의 학습

● Vanilla Gradient Descent : Gradient를 한번 업데이트 하기 위해 모든 학습 데이터를 사용한다.

● Stochastic GD (SGD) : Gradient를 한번 업데이트 하기 위해 일부의 데이터만 사용한다.

● Mini-Batch 학습법 : 학습 데이터 전체를 한번 학습하는 것을 Epoch, 한 번 Gradient를 구하는 단위를 Batch


※ Vanilla Gradient Descent는 확률적 기울기(Stochastic Gradient)보다 실제 기울기가 더 좋은 결과가 나타난다. 그럼에도 SGD를 사용하는 이유는 Gradient를 한 번 Update하는 데 걸리는 시간이 수천 배 이상 차이가 나기 때문 + SGD에서 Gradient의 질이 떨어지는 부분은 심화 최적화 알고리즘으로 커버 가능!!
◎ 데이터셋의 구성
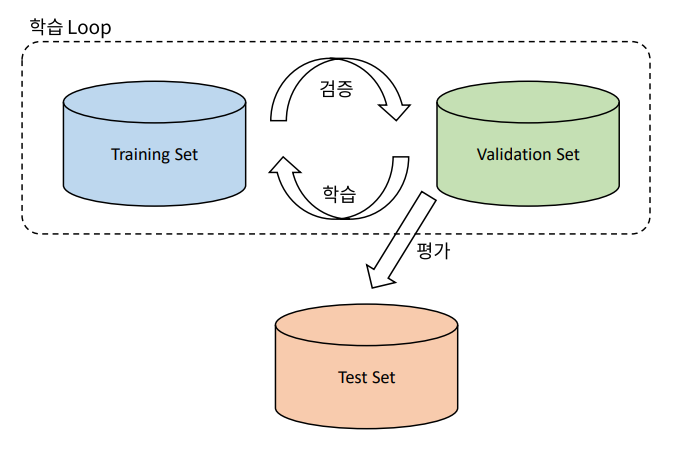
● 학습 데이터 : 실제 모델을 학습하는 데에 사용되는 데이터
● 검증 데이터 : 학습이 잘 되고 있는지 검증하는 데에만 사용
● 테스트 데이터 : 학습을 마친 모델을 평가하기 위해 단 한번만 보여지는 데이터
◎ 매개 변수의 종류

◎ 과대적합, 과소적합

※ 학습 조기 종료 (Early Stopping) : Validation loss가 여러 Epoch 동안 감소하지 않으면 Overfitting으로 간주하여 학습을 중단
◎ Drop-Out : 일정 확률로 뉴런을 제거하는 기법


※ 일부의 특징만을 사용해서도 좋은 결과를 낼 수 있다. 각각의 가능성에 대해 좋은 결과를 내도록 학습할 결우, 이를 평균하면 (Ensemble) 균형있는 결과를 얻을 수 있다. 즉, 어느 특정한 Feature에 집중하여 Overfitting 되는 결과를 막아준다.
◎ 합성곱 신경망
- LTI 선형 시불변 시스템(Linear Time Invariant System) : 선형적이고 시간에 영향 받지 않는 신호처리 시스템

※ LTI 시스템에 임펄스(Dirac 델타 함수)를 입력했을 때의 출력을 임펄스 응답이라고 한다. 임펄스 응답을 필터(Filter)라고도 하며, LTI 시스템의 동작을 완전하게 표현한다.
● 합성곱 연산(Convolution) : 두 함수를 합성하는 합성곱 연산, 한 함수를 뒤집고 이동하면서, 두 함수의 곱을 적분하여 계산

● 영상의 합성곱 계산 : 2-D 디지털 신호의 합성곱은 필터를 한 칸씩 옮기면서 영상과 겹치는 부분을 모두 곱해 합치게 된다.
+ 합성곱 연산 시, 필터(커널)의 크기에 따라 영상의 크기가 줄어드는 문제가 있다.

● Zero-Padding : 영상의 크기가 줄어드는 문제를 해결하는 Zero-Padding

● Stride : 합성곱 연산에서 커널을 이동시키는 거리를 Stride라고 하며, 이를 크게 하면 출력의 크기가 줄어든다.

● 잡음 제거 필터 : 2-D Gaussian Filter를 적용하면 흐려진 영상을 얻을 수 있다. 잡음을 제거하는 특성이 있다.
● 미분 필터 : Sobel Filter를 적용하면 특정 방향으로 미분한 영상을 얻을 수 있다. 해당 방향의 Edge 성분을 추출하는 특성이 있다.
◎ 합성곱 계층
- 합성곱으로 이루어진 뉴런을 전결합 형태로 연결한 것을 합성곱 계층이라고 한다.
- 여러 채널에서 특별한 '특징'이 나타나는 위치를 찾아내는 것이 합성곱 계층의 역할
◎ 풀링 계층
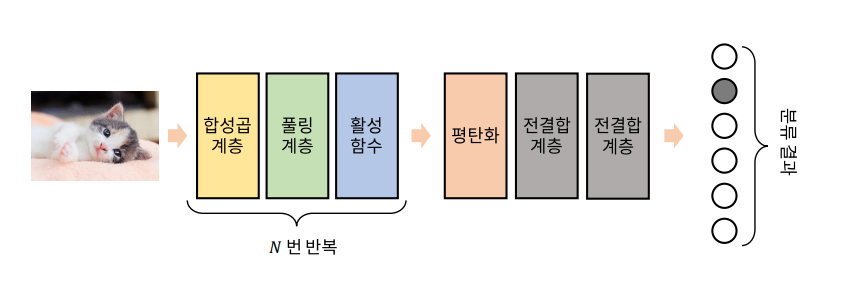
- 합성곱 계층에서는 영상의 크기는 그대로이며, 영상의 채널 수가 달라진다.
- 합성곱 계층에 의해서 추출된 결과는 공간적 특징이 있으며 '특징 맵(Feature Map)'이라고 한다.
○ 풀링 계층은 여러 화소를 종합하여 하나의 화소로 변환하는 계층이다. 풀링 계층을 통과하면 영상의 크기가 줄어들고, 정보가 종합된다.


※ 합성곱 신경망의 애플리케이션에 맞는 풀링 계층을 사용한다.

◎ LeNet-5

◎ AlexNet
- 특정 계층들에서만 GPU간의 정보 교환이 이루어지는 것이 특징
- Local Response Normalization : ReLU를 사용하였을 때, 양수 방향으로 무한히 커질 수 있는 점을 보완


◎ Vanilla RNN
● 순차 데이터 (Sequential Data) : 순서가 의미가 있으며, 순서가 달라질 경우 의미가 손상되는 데이터를 순차 데이터
+ 시간적 의미가 있는 경우 Temporal Sequence라고 하며, 일정한 시간차라면 Time Series라고 한다.

※ 음성에 대한 올바른 대답을 하려면, 입력을 받을 때 마다 그 내용을 '기억'할 수 있어야 한다. 이전 입력을 기억하지 않는 시스템은 무기억 시스템(Memoryless System)이라 한다.
● 얕은 신경망(Shallow Neural Network)
- 대표적인 무기억 시스템인 얕은 신경망
- 무기억 시스템이므로 n번째 타입 스텝에 대한 결과가 이전 입력에 영향을 받지 않는다.

● 기본적인 순환 신경망(Vanilla RNN)
- 얕은 신경망 구조에 '순환'이 추가된 것
- 기억 시스템이므로, RNN의 출력은 이전의 모든 입력에 영향을 받는다.

● 다중 계층 순환 신경망(Multi-Layer RNN)
- 순환 신경망도 심층 신경망처럼 쌓아 올릴 수 있다.
- 구조가 매우 복잡해지고 학습이 잘 되지 않아, 권장하지 않는다.

※ 순환 신경망은 기본 역전파 학습법으로는 학습할 수 없다.
+ 입력 또는 출력 중 하나라도 순차 데이터라면, 순환 신경망을 이용해 학습할 수 있다.
● 다중 입력, 단일 출력의 학습
- 순방향 추론시에는, 입력을 순차적으로 입력하여 마지막 입력시의 출력을 사용한다.
- 역전파와 동일하게, 시간적으로 펼쳐 둔 상태에서 역전파를 한다.
- 이 때, 시간적으로 펼쳐진 변수들은 동일한 변수라는 점에 유의해야 한다.

● 다중 입력, 다중 출력
- 입력과 출력이 매 Time-Step 마다 이루어지는 경우, 동영상의 프레임별 분류를 예로 들수 있다.
- 모든 입력을 받은 후에 출력을 내는 경우. 문장 번역, 챗봇 등의 애플리케이션이 있다.

'Data scientist > Deep Learning' 카테고리의 다른 글
| Deep Learning_3 (0) | 2021.09.21 |
|---|---|
| Deep Learning_1 (0) | 2021.09.15 |